References

Using kernel density methods for estimating range size comes from a series of papers by Worton: (Worton_1989?; Worton_1989a?; Worton_1995?). The kernel density estimates are calculated using the adehabitatMA package (Calenge_2006?). The theoretical approach is presented in Broennimann et al. (2012), and implemented in the ecospat package (Cola et al., 2017). (PhillipsElith_2010?) provides useful discussion, the niche dynamic plots of ecospat are one form of what they refer to as “Presence-Only Calibration Plots” (PCO-plots).

Setup

We need the ecospat, ade4, and raster packages for this analysis:

library(ecospat)
library(ade4)
library(raster)

Data Preparation

Required preliminary data are ordination scores for the total environment (i.e., the entire range of both species), the local environment (i.e., the ranges of each species of interest), and the PCA scores for each species of interest. The ordination space is defined by the background environment, the species scores are supplemental.

data(ecospat.testNiche)
data(ecospat.testData)

  ## The coordinates for two different species:
sp1 <- subset(ecospat.testNiche, 
             Spp == levels(ecospat.testNiche$Spp)[1])
sp2 <- subset(ecospat.testNiche, 
             Spp == levels(ecospat.testNiche$Spp)[2])

  ## The environmental data for 300 locations: 
clim <- ecospat.testData[2:8]

  ## Add environmental data to species data:
sp1 <- cbind(sp1,
            na.exclude(
              ecospat.sample.envar(dfsp = sp1,
                                   colspxy = 2:3,  
                                   colspkept = 1:3,
                                   dfvar = clim,
                                   colvarxy = 1:2,
                                   colvar = "all",
                                   resolution = 25)))

sp2 <- cbind(sp2,
            na.exclude(
              ecospat.sample.envar(dfsp = sp2,
                                   colspxy = 2:3, 
                                   colspkept = 1:3,
                                   dfvar = clim, 
                                   colvarxy = 1:2,
                                   colvar = "all",
                                   resolution = 25)))

##########################################################
## NB. `ecospat.sample.envar` samples from a data.frame ##
## of points, analogously to how `extract` samples from ##
## raster layer.                                        ##
##########################################################

  ## selection of variables to include in the analyses
Xvar <- c("ddeg", "mind", "srad", "slp", "topo")
nvar <- length(Xvar)

pca.cal <- dudi.pca(clim[, Xvar], center = TRUE,
                   scale = TRUE, scannf = FALSE, nf = 2)

  ## Species scores:
sp1.scores <- suprow(pca.cal, sp1[, Xvar])$li
sp2.scores <- suprow(pca.cal, sp2[, Xvar])$li
scores.clim <- pca.cal$li

  ## scores.sp1 and scores.sp2 now contain the position of  
  ## these two species in the environmental ordination
  ## space. 

Let’s take a look at the starting data:

plot(scores.clim, pch = 16, asp = 1,
     col = adjustcolor(1, alpha.f = 0.2), cex = 2,
     xlab = "PC1", ylab = "PC2") 
points(sp1.scores, pch = 17, col = 2, cex = 2)
points(sp2.scores, pch = 18, col = 4, cex = 2)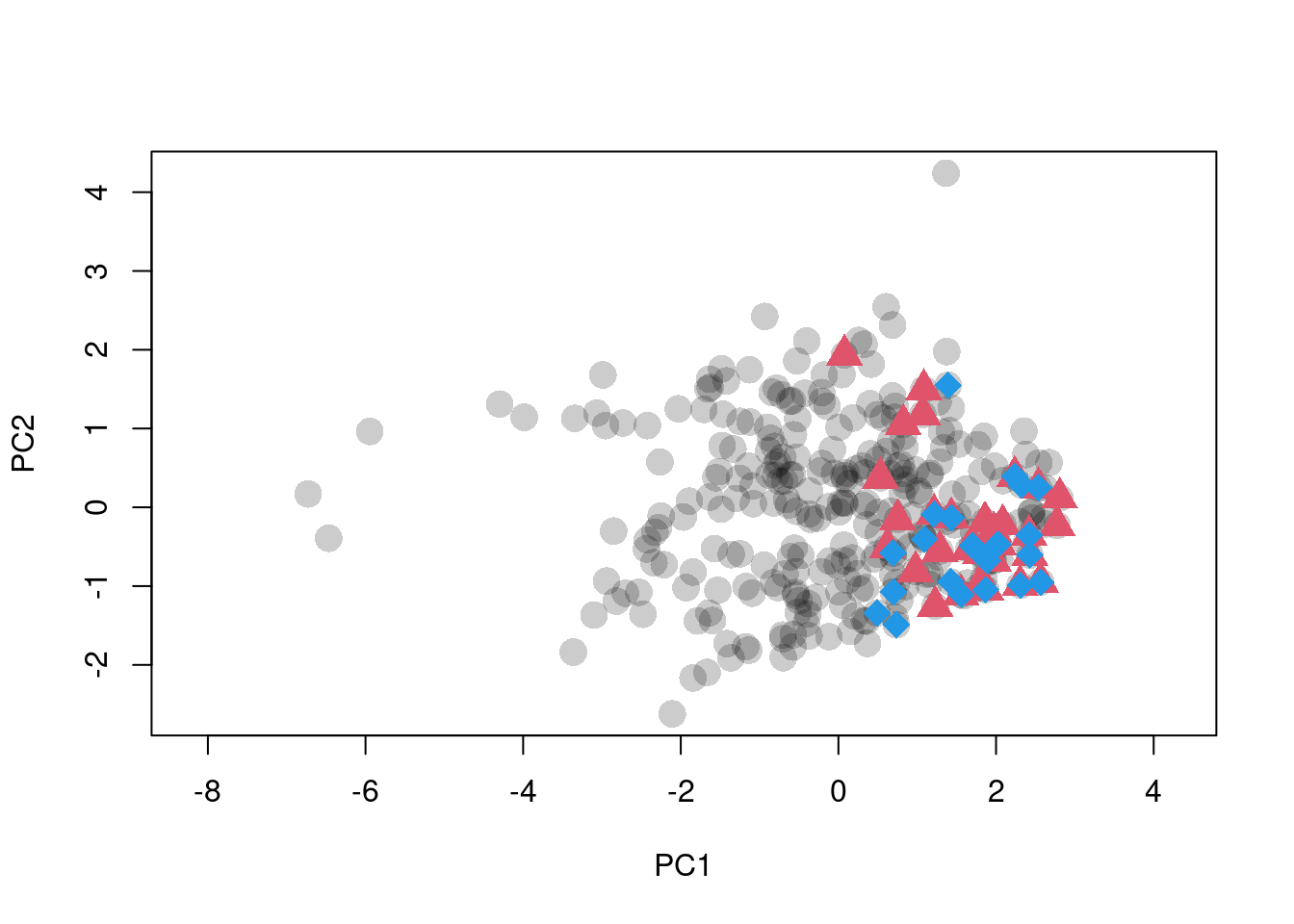

Figure 1: Ordination of raw climate data. Black dots are background points. Red triangles and blue diamonds are species occurences.

Kernel Density Estimates

Next we create the occurence density grids for the two species we wish to compare. These grids are called gridclim objects in the ecospat documentation (not really objects in the R sense, just lists).

We feed the ordination data to ecospat.grid.clim.dyn to get the actual grids:

z1 <- ecospat.grid.clim.dyn(scores.clim, scores.clim,
                            sp1.scores, R = 100)

## Registered S3 methods overwritten by 'adehabitatMA':
##   method                       from
##   print.SpatialPixelsDataFrame sp  
##   print.SpatialPixels          sp

z2 <- ecospat.grid.clim.dyn(scores.clim, scores.clim,
                           sp2.scores, R = 100)

This does the following:

• the extent is set to the limits of the global environment
• the kernel density of the local environment is estimated
• the kernel density of the species occurence environment is estimated

Various transformations and corrections are applied to these estimates. The list that is returned contains:

• x, y : the coordinates for each cell in the resulting density plot
• z : the occurence density estimate for each cell in the plot, scaled to the total number of occurences in the raw data
• z.uncor : z scaled to 0-1. i.e., the density estimate for a cell is a direct reflection of the number of occurences in the vicinity of that cell, regardless of the environmental distribution.
• z.cor : z corrected for environmental prevalence i.e., we take the density estimate, and divide by the relative abundance of the environment at that location. Effectively, we need more occurences at common environments to achieve the same density estimate as a smaller number in a rare environment.
• Z : the home/local environment density estimate for each cell in the plot, scaled to the total number of rows in the raw environment data (background)
• w : the “niche envelope”, which is z.uncor converted to a presence-absence map (all values > 0 become present).
• glob, glob1, sp : the coordinates of all observations in the raw global environment, raw local environment, and species occurence data

The key outputs are z.uncor and z.cor. We can compare these with a few plots:

par(mfrow = c(2, 2), mar = c(0.5, 0.5, 2, 0))
plot(z1$z.uncor, legend = FALSE, axes = FALSE,
     main = "z.uncor - Full")
points(z1$sp, pch = 16, col = adjustcolor(1, alpha.f = 0.5))
plot(z1$z.cor, legend = FALSE, main = "z.cor - Full",
     axes = FALSE) 
points(z1$sp, pch = 16, col = adjustcolor(1, alpha.f = 0.5))
plot(z1$z.uncor, xlim = c(0, 3), ylim = c(-2, 2),
     axes = FALSE, legend = FALSE, main = "z.uncor - Zoom")
points(z1$sp, pch = 16, col = adjustcolor(1, alpha.f = 0.5))
plot(z1$z.cor, xlim = c(0, 3), ylim = c(-2, 2), axes = FALSE,
     legend = FALSE, main = "z.cor - Zoom")
points(z1$sp, pch = 16, col = adjustcolor(1, alpha.f = 0.5))

We can see that z-uncor looks like we expect. The observations are arranged in a circular cloud, which is captured as a circular-shaped kernel density. In contrast, z.cor shows a higher kernel density estimate in the lower right corner, despite using the same observations. The reason is that the observations in the lower right occur in rarer environments, so they are given higher relative weight in the density estimate. Here’s the environmental density:

plot(z1$Z, axes = FALSE, legend = FALSE, 
     main = "Environmental density - Full")
points(z1$sp, pch = 16, col = adjustcolor(1, alpha.f = 0.5))

The green area shows the most common environments. The observations within this area are given reduced weight relative to the observations in rare environments (the pink areas on the margin). This creates the ‘skew’ in the corrected occurence density kernel.

glob1.dens <- ecospat.kd(x = glob1, ext = ext,
                         method = kernel.method, th = 0)

R <- 100 # grid size
xmin <- apply(scores.clim, 2, min, na.rm = T)
xmax <- apply(scores.clim, 2, max, na.rm = T)
ext <- c(xmin[1], xmax[1], xmin[2], xmax[2])

## Scale the raw coordinates to 0-1:
xr <- data.frame(
  cbind(
  (scores.clim[, 1] - ext[1]) / abs(ext[2] - ext[1]),
  (scores.clim[, 2] - ext[3]) / abs(ext[4] - ext[3])))

mask <- adehabitatMA::ascgen(
                       sp::SpatialPoints(cbind((0:(R)) / R,
                       (0:(R) / R))), nrcol = R - 2,
                       count = FALSE) 

x.UD <- adehabitatHR::kernelUD(sp::SpatialPoints(xr[, 1:2]),
                                h = "href", grid = mask,
                                kern = "bivnorm"
                                )

## Shift the density back to match the original projection:
x.dens <- raster::raster(
                   xmn = ext[1], xmx = ext[2], ymn = ext[3],
                   ymx = ext[4], matrix(x.UD$ud, nrow = R)
                 )
  
plot(x.dens)
points(scores.clim)

x.dens.ls <- 
  adehabitatHR::kernelUD(sp::SpatialPoints(xr[, 1:2]),
                         h = "LSCV", grid = mask,
                         kern = "bivnorm")   
x.dens.ls <-
  raster::raster(xmn = ext[1], xmx = ext[2], ymn = ext[3],
                 ymx = ext[4], matrix(x.dens.ls$ud,
                                      nrow = R))

#dev.new(width = 6, height = 8)

par(mfrow = c(2, 2), mar = c(2, 0.1, 3, 0))
plot(x.dens, main = "Ad Hoc", legend = FALSE, axes = FALSE)
points(scores.clim, pch = 16, cex = 0.5,
       col = adjustcolor("black", alpha.f = 0.1))
plot(x.dens.ls, main = "LSCV", legend = FALSE, axes = FALSE)
points(scores.clim, pch = 16, cex = 0.5,
       col = adjustcolor("black", alpha.f = 0.1))

plot(x.dens, main = "Ad Hoc", legend = FALSE, axes = FALSE,
     xlim = c(-1, 2), ylim = c(-1, 1))
plot(x.dens.ls, main = "LSCV", legend = FALSE, axes = FALSE,
     xlim = c(-1, 2), ylim = c(-1, 1))

## Shift the raw data to match the extent:
spec1r <- data.frame(
  cbind(
  (sp1.scores[, 1] - ext[1]) / abs(ext[2] - ext[1]),
  (sp1.scores[, 2] - ext[3]) / abs(ext[4] - ext[3])))

sp1.dens <- adehabitatHR::kernelUD(sp::SpatialPoints(spec1r[, 1:2]),
                                h = "href", grid = mask,
                                kern = "bivnorm") 
sp1.dens <- raster::raster(
                     xmn = ext[1], xmx = ext[2], ymn = ext[3],
                     ymx = ext[4], matrix(sp1.dens$ud, nrow = R))
  
sp1.dens.ls <- adehabitatHR::kernelUD(sp::SpatialPoints(spec1r[, 1:2]),
                                   h = "LSCV", grid = mask,
                                   kern = "bivnorm") 
sp1.dens.ls <- raster::raster(
                      xmn = ext[1], xmx = ext[2], ymn = ext[3],
                      ymx = ext[4], matrix(sp1.dens.ls$ud,
                      nrow = R))

par(mfrow = c(2, 2), mar = c(2, 0.1, 3, 0))
plot(sp1.dens, main = "Ad Hoc", legend = FALSE, axes = FALSE)
points(sp1.scores, pch = 16, cex = 0.5,
       col = adjustcolor("black", alpha.f = 0.1))
plot(sp1.dens.ls, main = "LSCV", legend = FALSE, axes = FALSE)
points(sp1.scores, pch = 16, cex = 0.5,
       col = adjustcolor("black", alpha.f = 0.1))
plot(sp1.dens, main = "Ad Hoc", legend = FALSE, axes = FALSE,
     xlim = c(-1, 1), ylim = c(1, 2.5))
points(sp1.scores, pch = 16, cex = 0.5,
       col = adjustcolor("black", alpha.f = 0.1))
plot(sp1.dens.ls, main = "LSCV", legend = FALSE, axes = FALSE,
     xlim = c(-1, 1), ylim = c(1, 2.5))
points(sp1.scores, pch = 16, cex = 0.5,
       col = adjustcolor("black", alpha.f = 0.1))

sp1.trim <- sp1.scores[1:7, ]
trimr <- data.frame(
  cbind(
  (sp1.trim[, 1] - ext[1]) / abs(ext[2] - ext[1]),
  (sp1.trim[, 2] - ext[3]) / abs(ext[4] - ext[3])))

trim.dens <-
  adehabitatHR::kernelUD(sp::SpatialPoints(trimr[, 1:2]),
                         h = "href", grid = mask,
                         kern = "bivnorm") 
trim.dens <-
  raster::raster(xmn = ext[1], xmx = ext[2], ymn = ext[3],
                 ymx = ext[4], matrix(trim.dens$ud, nrow = R))
  
trim.dens.ls <-
  adehabitatHR::kernelUD(sp::SpatialPoints(trimr[, 1:2]),
                         h = "LSCV", grid = mask,
                         kern = "bivnorm") 
trim.dens.ls <- raster::raster(
                      xmn = ext[1], xmx = ext[2], ymn = ext[3],
                      ymx = ext[4], matrix(trim.dens.ls$ud,
                      nrow = R))

par(mfrow = c(2, 2), mar = c(2, 0.1, 3, 0))
xlims <- c(0, 5)
ylims <- c(-1, 2)
plot(trim.dens, main = "Ad Hoc", legend = FALSE, axes = FALSE)
points(sp1.trim, pch = 16, cex = 1,
       col = adjustcolor("black", alpha.f = 0.4))
plot(trim.dens.ls, main = "LSCV", legend = FALSE, axes = FALSE)
points(sp1.trim, pch = 16, cex = 1,
       col = adjustcolor("black", alpha.f = 0.4))
plot(trim.dens, main = "Ad Hoc", legend = FALSE, axes = FALSE,
     xlim = xlims, ylim = ylims)
points(sp1.trim, pch = 16, cex = 1,
       col = adjustcolor("black", alpha.f = 0.4))
plot(trim.dens.ls, main = "LSCV", legend = FALSE, axes = FALSE,
     xlim = xlims, ylim = ylims)
points(sp1.trim, pch = 16, cex = 1,
       col = adjustcolor("black", alpha.f = 0.4))

Niche expansion, stability, and unfilling

Once we have our grids, we proceed to calculate the dynamic niche indices. Assume we’re comparing two species, sp1 and sp2, each with their own ‘native’ environment env1 and env2. The global environment globenv is just env1 and env2 combined. In the case of species with the same range (i.e., comparing 2 North American species), env1 = env2 = globenv.

We have all the grids available now: w, z.cor, z.uncor, Z, for both species, in the results returned by ecospat.grid.clim.dyn. We can pass this on to ecospat.niche.dyn.index to generate the metrics of interest:

ind1 <- ecospat.niche.dyn.index(z1, z2)

The first step in this process is categorizing each cell in the ordination as expansion, stability, or unfilling. This is determined using only the presence/absence layers, w:

## Convert to matrices to allow us to do logical operations:
w1 <- as.matrix(z1$w)
w2 <- as.matrix(z2$w)

stability <- w1 & w2   ## both present
expansion <- w2 & ! w1 ## only sp2 present
unfilling <- w1 & ! w2 ## only sp1 present

## Combine: expansion = 1, unfilling = 2, stablility = 3)
dyn.index <- expansion + (2 * unfilling) + (3 * stability)

## rotate the matrix so the image is oriented properly:
dyn.index <- t(apply(dyn.index, 2, rev))

## visualize:
image(dyn.index, col = c("#FFFFFF", "red", "blue", "green"),
      axes = FALSE)  
box()

For visualization, we can do this all in one operation:

cr <- colorRampPalette(c("white", "red", "green", "blue"))
plot(2*z1$w+z2$w, col = cr(4))
points(z1$sp, pch = 21, bg = "green", col = 1)
points(z2$sp, pch = 21, bg = "red", col = 1)

To explain this trick: we add the two maps together, with the first map counting twice. The result is, any cell with the value 1 means only the corresponding cell in the second map was occupied. 2 means only the first map is occupied. 3 is both maps occupied.

Computation aside, the categorization of pixels is straightforward to interpret.

But wait! We can’t just sum up the different categories to get our indices. Each cell is weighted before we compute the indices. Applying the same trick, the calculations proceed as follows:

## Create a raster with the classified pixels:
dyn.raster <- 2*z1$w+z2$w

## Extract the three categories:
exp.raster <- dyn.raster == 1
unfill.raster <- dyn.raster == 2
stab.raster <- dyn.raster == 3

## Compute their weights:
exp.weighted <- z2$z.uncor * exp.raster
## stability also weighted by species 2:
stab.weighted <- z2$z.uncor * stab.raster
## unfilling weighted by species 1:
unfill.weighted <- z1$z.uncor * unfill.raster
## but we need stability weighted by species 1 too: 
stab1.weighted <- z1$z.uncor * stab.raster

## Calculate indices:

expansion.index <- sum(getValues(exp.weighted)) /
  sum(getValues(exp.weighted + stab.weighted))

stability.index <- sum(getValues(stab.weighted)) /
  sum(getValues(exp.weighted + stab.weighted))
## alternatively, 1 - expansion.index

unfilling.index <- sum(getValues(unfill.weighted)) /
  sum(getValues(unfill.weighted + stab1.weighted))

And the values I get from my re-implementation of ecospat match exactly:

My indices: Expansion: 0.060, Stability: 0.940, Unfilling: 0.136

Ecospat indices: Expansion: 0.060, Stability: 0.940, Unfilling: 0.136