Data

I use the same GBIF records previously downloaded in my Ecospat with Terra tutorial.

library(terra)
library(geodata)
library(rgbif) ## not actually necessary, used to download
               ## the occurrence data

library(usdm) ## for vif collinearity test below

load("../data/2021-07-29-ls-gbif-recs.Rda")
lsOccs <- lsGBIF$data

## convert to a spatial vector:
lsOccs <- vect(lsOccs, geom = c("decimalLongitude",
                                "decimalLatitude"),
               crs = "+proj=longlat +datum=WGS84")

wrld <- world(path = "../data/maps/")

wclim <- worldclim_global(var = "bio", res = 10,
                          path = "../data/")

## North America basemap:
nAmCountries <- c("CAN", "MEX", "USA")
nAm <- gadm(nAmCountries, level = 0,
            path = "../data/maps/",
            resolution = 2)

## Eurasia basemap:
eurasiaCountries <- country_codes("Asia|Europe")

## remove missing countries:
eurasiaCountries <-
  eurasiaCountries[!eurasiaCountries$ISO3 %in%
                    c("HKG", "MAC", "XNC"),] 
eur <- gadm(eurasiaCountries$ISO3, level = 0,
            path = "../data/maps/",
            resolution = 2)

## subset occurrences
lsNA <- lsOccs[nAm]
lsEA <- lsOccs[eur]

Training Region

There are a number of considerations when deciding on the region to use to train our model. For this example, I’ll just use a 500km buffer around occurrences in the native range.

Now we have all the data we need for the analysis:

train <- buffer(lsEA, width = 500000)
train <- aggregate(train)

plot(wrld, mar = c(1.5, 1.5, 0.5, 0.5))
plot(train, col = '#00FF0080', add = TRUE)
plot(lsEA, add = TRUE, cex = 0.5)
plot(lsNA, add = TRUE, cex = 0.5, col = 'blue')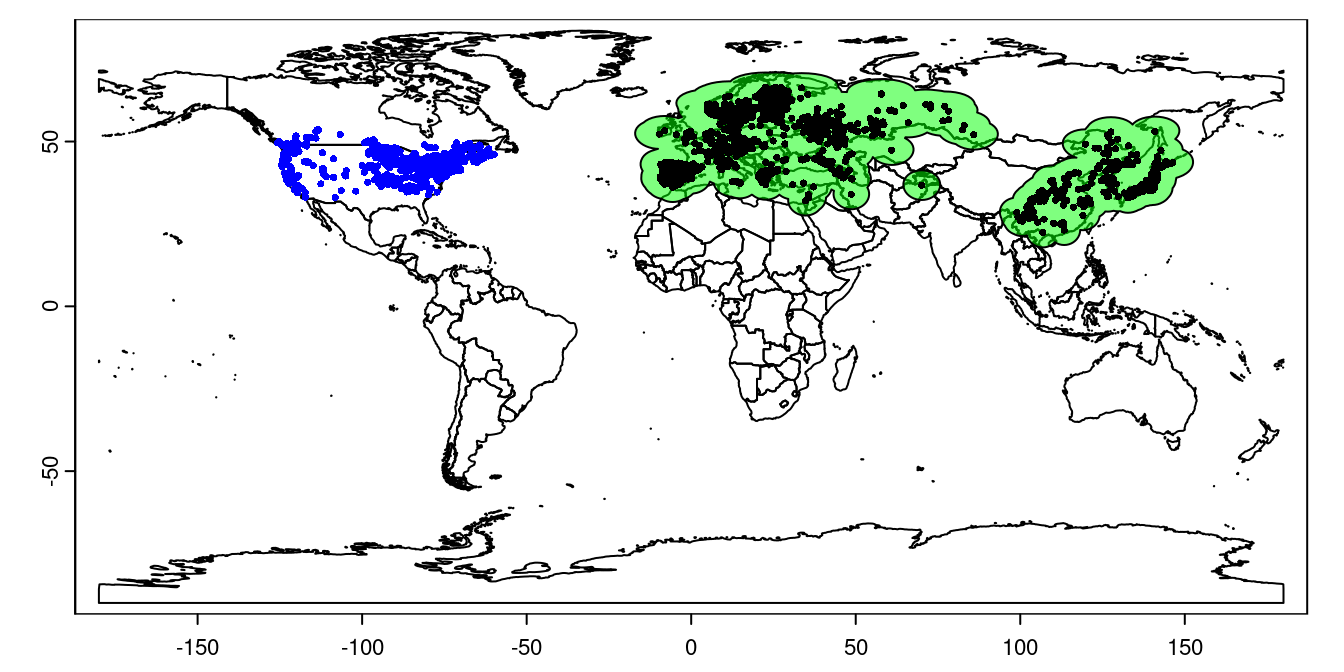

Figure 1: Lythrum salicaria distribution. Green shading shows the training region, black points are occurrences in the native range, and blue points are occurrences in the invaded range.

Note that the training region extends into the ocean, but the underlying worldclim data doesn’t, so we don’t need to worry about cleaning this up.

Mahalanobis Distance

Now we can calculate the NT2 index. We start by clipping the climate data to our training and projection regions, and then selecting a set of variables that aren’t highly collinear (in the training region):

trainWC <- mask(wclim, train)
trainVal <- values(trainWC)

naWC <- mask(wclim, nAm)
naVal <- values(naWC)

## screen out collinear variables:
vifSel <- vifstep(data.frame(trainVal), th = 5,
                  size = 20000)

VARS <- vifSel@results$Variables

VARS contains a list of non-collinear variables. For a real analysis you probably should be more deliberate in selecting which variables to retain, in order to consider both their biological interest and statistical properties.

trainMeans <- colMeans(trainVal[, VARS], na.rm = TRUE)
trainVar <- var(trainVal[, VARS], na.rm = TRUE)
trainMah <- mahalanobis(trainVal[, VARS], trainMeans,
                        trainVar, na.rm = TRUE)

trainMah now contains the Mahalanobis distance from each cell in the training region to the climate centroid of the training region. ‘0’ means the point is in the center of the climate space. By the nature of the Mahalanobis distance, this value accounts for covariation among our climate variables.

As a quick check, let’s take a look at the Mahalanobis distances for the training region:

hist(trainMah, main = "Mahalanobis Distances in Eurasia",
     xlab = "Distance")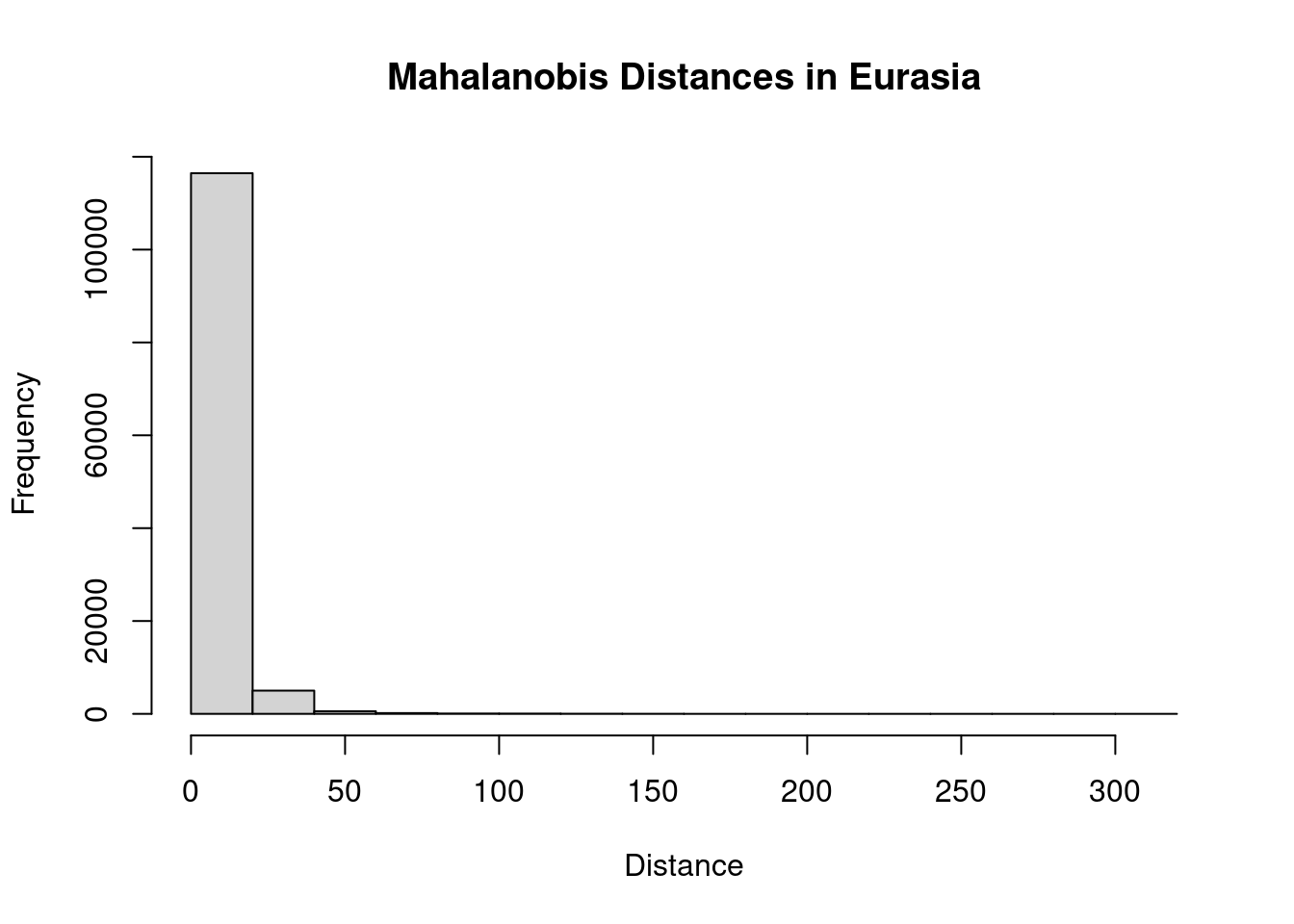

That’s a bit odd. We have a small number of outliers with very high distances. I think this is likely a consequence of idiosyncracies in our climate rasters: an artifact of the analysis rather than a biologically meaningful value. To clean this up, I’ll identify values above the 95th percentile as outliers and remove them. Then we can proceed with calculating the distances for the invaded range.

thresh <- quantile(trainMah, probs = 0.95, na.rm = TRUE)
trainMah[which(trainMah > thresh)] <- NA
hist(trainMah, main = "Trimmed Mahalanobis Distances in Eurasia",
     xlab = "Distance")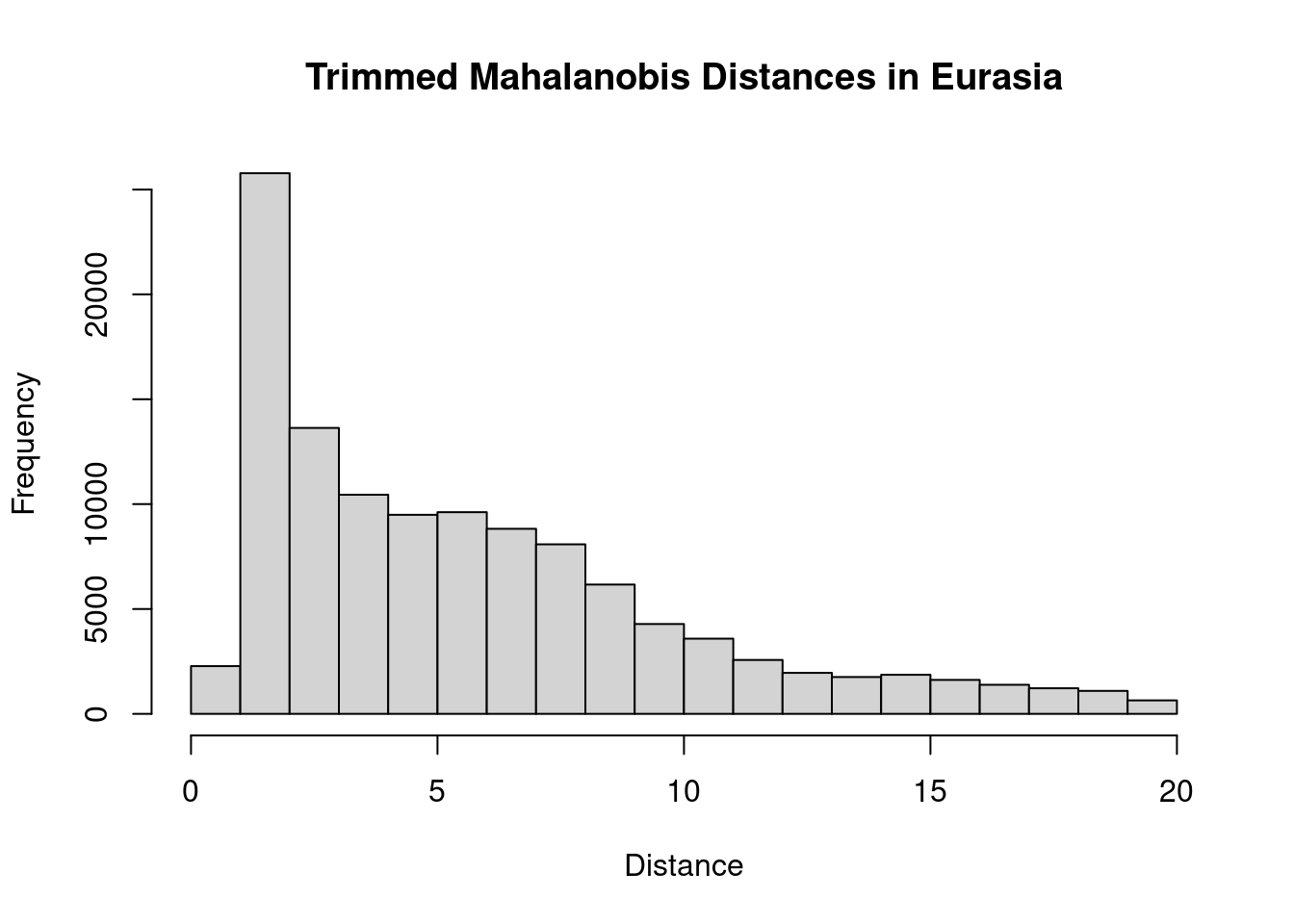

That looks better. Moving on, we can now calculate NT2, which is the Mahalanobis distance divided by the maximum Mahalanobis distance in the training range:

maxMah <- max(trainMah, na.rm = TRUE)
trainMah <- trainMah/maxMah
trainMahR <- trainWC[[1]]
values(trainMahR) <- trainMah

naMah <- mahalanobis(naVal[, VARS], 
                     trainMeans, trainVar, na.rm = TRUE)
naMah <- naMah/maxMah

## Create a new raster map for North America:
naMahR <- naWC[[1]]

## set the values to our Mahalanobis distances:
values(naMahR) <- naMah

Now we have a raster map with the NT2 index values for each cell in the training and invaded ranges. Values between 0 and 1 are within the training range. We can visualize that directly:

COLS <- c("green", "lightgreen", "aquamarine", "blue", 
           "orange", "brown", "red")

BREAKS = c(0, 0.25, 0.5, 1, 2, 4, 8, 16)

plot(trainMahR, breaks = BREAKS, col = COLS,
     mar = c(2, 2, 1, 5))
plot(naMahR, breaks = BREAKS, col = COLS, add = TRUE, legend
     = FALSE)
plot(wrld, border = 'lightgrey', add = TRUE, lwd = 0.5)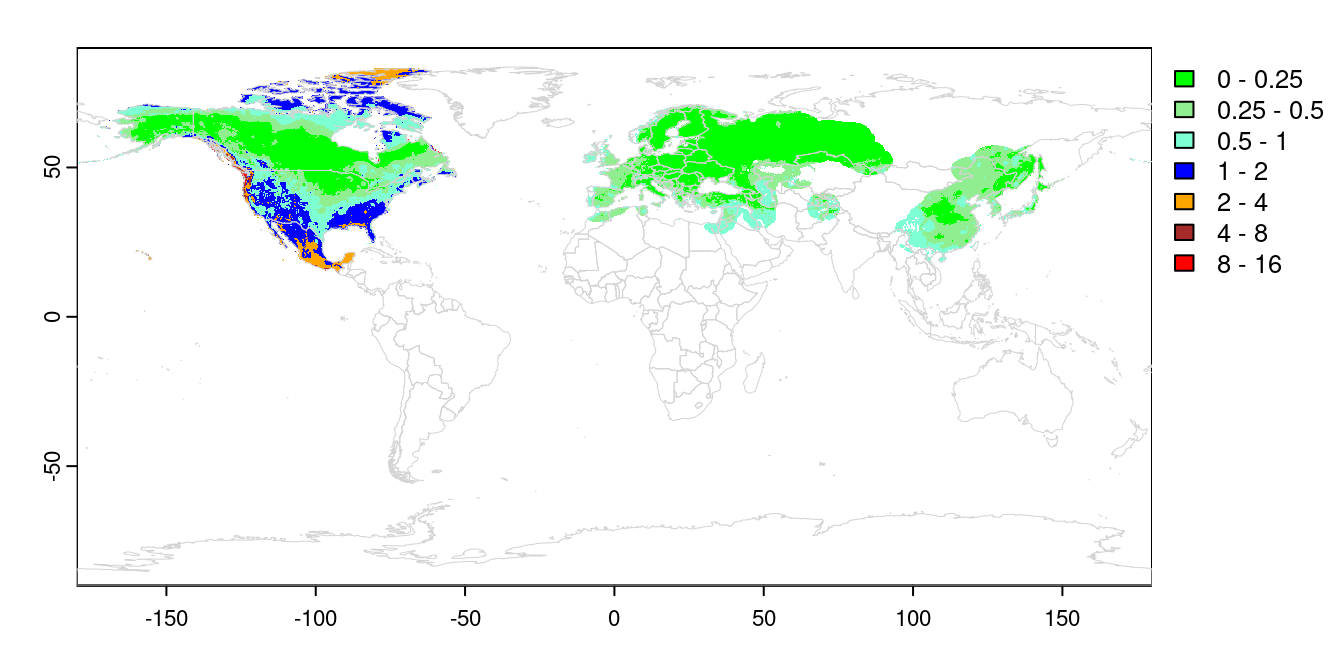

This completes main part of the exDet analysis. We can see the training range all falls within the range 0-1, which is by design. Transferring that distribution to North America, we can see most of Canada and the north central US falls within the same range. The high arctic, the SE US and western US are all outside of the training range, with Mexico even more novel. Projections into these areas should be treated with caution, or avoided entirely.

Most Influential Covariate, MIC

While the map above is our primary interest in exDet analysis, we may want to know which variables are most influential in creating novel environments. To do this, we need to calculate the distance map repeatedly, removing one variable at a time. For each cell, we can then identify the variable that contributes the most to its NT2 index, by calculating the difference between the distance for all variables, and the distance with that variable removed.

names(naMahR) <- "all"

## Remove variables one at a time and recalculate distances:

for(V in VARS){
  SEL <- VARS[VARS != V]

  tmpMeans <- colMeans(trainVal[, SEL], na.rm = TRUE)
  tmpVar <- var(trainVal[, SEL], na.rm = TRUE)
  tmpMah <- mahalanobis(trainVal[, SEL], tmpMeans,
                        tmpVar, na.rm = TRUE)

  thresh <- quantile(tmpMah, probs = 0.95, na.rm = TRUE)
  tmpMah[which(tmpMah > thresh)] <- NA
  tmpMax <- max(tmpMah, na.rm = TRUE)

  resMah <- mahalanobis(naVal[, SEL], 
                     tmpMeans, tmpVar, na.rm = TRUE)
  resMah <- resMah/tmpMax
  resMahR <- naWC[[1]]
  
  ## calculate difference from full distance:
  values(resMahR) <- values(naMahR$all) - resMah

  ## add a layer to our NA raster:
  naMahR[[V]] <- resMahR
}

## Find the maximum difference for each cell:
naMaxMah <- max(naMahR[[-1]])
naTest <- naMahR[[-1]] == naMaxMah

## Convert TRUE/FALSE to category numbers:

for(L in seq_along(names(naTest))){
  values(naTest[[L]]) <- values(naTest[[L]]) * L
}

## Collapse layers into a single raster:
naCat <- max(naTest)

## convert to a factor
levs <- data.frame(vals = seq_along(VARS),
                   ## clean up variable names:
                   levels = gsub("wc2.1_10m_", "", VARS))
levels(naCat) <- levs

Now we can visualize which individual variables are contributing most to the NT2 index for each cell:

plot(naCat, xlim = c(-180, -40), ylim = c(10, 90),
     mar = c(2, 2, 4, 5),
     main = "Most Influential Covariate")
plot(wrld, border = 'lightgrey', lwd = 0.5, add = TRUE)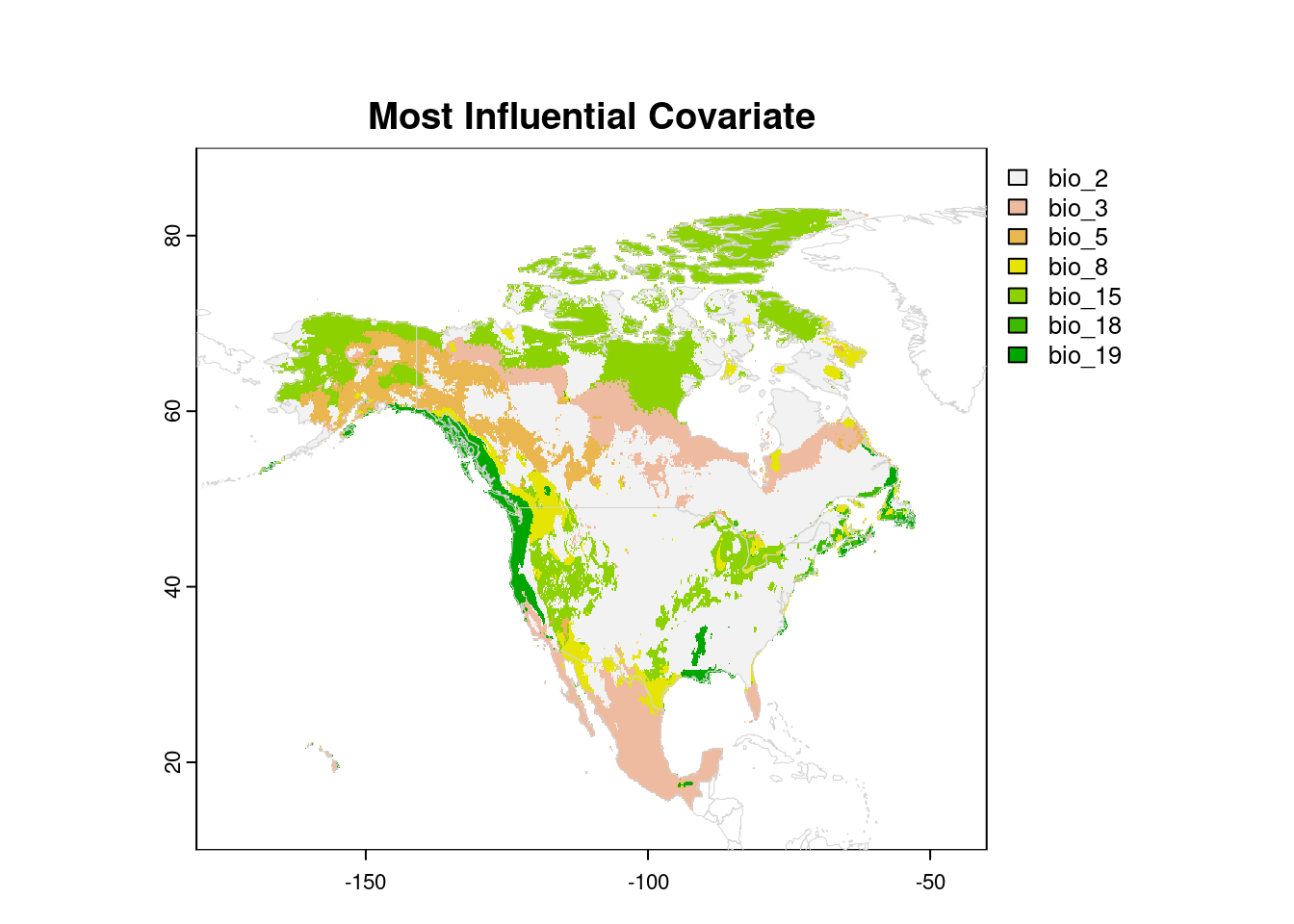

Whether or not that information is useful to you will depend on your research question, of course.